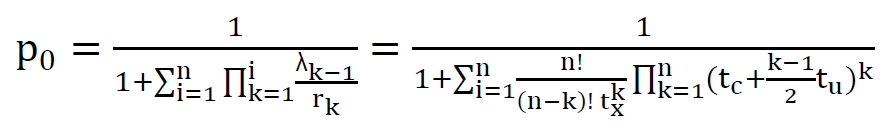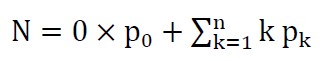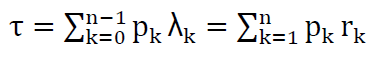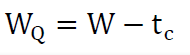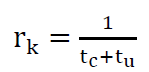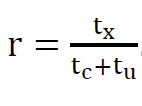Linux Spin Lock Limitation proof
by yy813 (CID 00848280)
This is a simple proof to some limitations to Linux Spin Lock mechanism. Please reference this post: https://yymath.github.io/2018/01/07/linux_spin_lock/. All rights reserved.
Step 1
When k cores are either using or queued on, the lock, corresponding arrival rate is: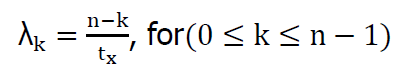 
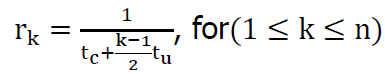
for 0 <= k <= n-1
Average cache-update time is proportional to the half of the total number of cores queued on the lock. Then we have the completion rate (output rate): 
for 1 <= k <= n
Step 2
Transition from state k is equal to the transition into the state k when the system is at the equilibrium. Then the general relationship (closed-form) between state k and state k+1 is: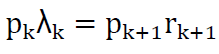 
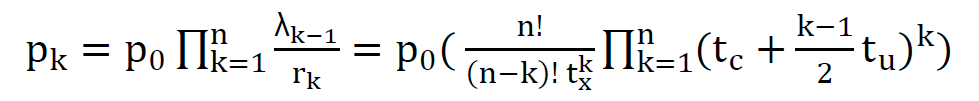
Therefore: 
which gives the general solution for state k in terms of probability of state 0. Since the total probability of all states is 1, where: 
Total population N (the mean number of cores either using or waiting for the lock) is: 
By definition, throughput is the product of completion rate multiplied by the probability of each state, which is also equal to the product of the arrival rate multiplied by corresponding probabilities: 
According to the Little’s Law: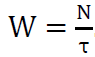 
Hence, the queuing time and the service time have the relationship: 
Step 3
From the coursework specification, “speed-up” can be expressed by: Speedup = n − N
Figure 1.1 and Figure 1.2 show the queuing time and speed-up against number of cores with different t𝑥.
Step 4
For an ideal ticket spinlock, completion rate becomes: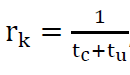 
for 1 <= k <=n
Corresponding speed-up with different number of cores are shown in Figure 1.3 (using the same equation for “speedup” and completion rate). The population is illustrated in Figure 2.2.
completion rate: 
Step 5
Collapse in the speed-up was observed in Figures 1.2 due to the average number of either executing or waiting cores (N) has been increasing faster than number of cores (n) itself. The main reason is the cache consistency which is assumed to be the bottle-neck of the spinlock tickets model. This is due to the fact that time to update every locally-cached copy of shared memory takes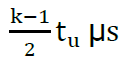 
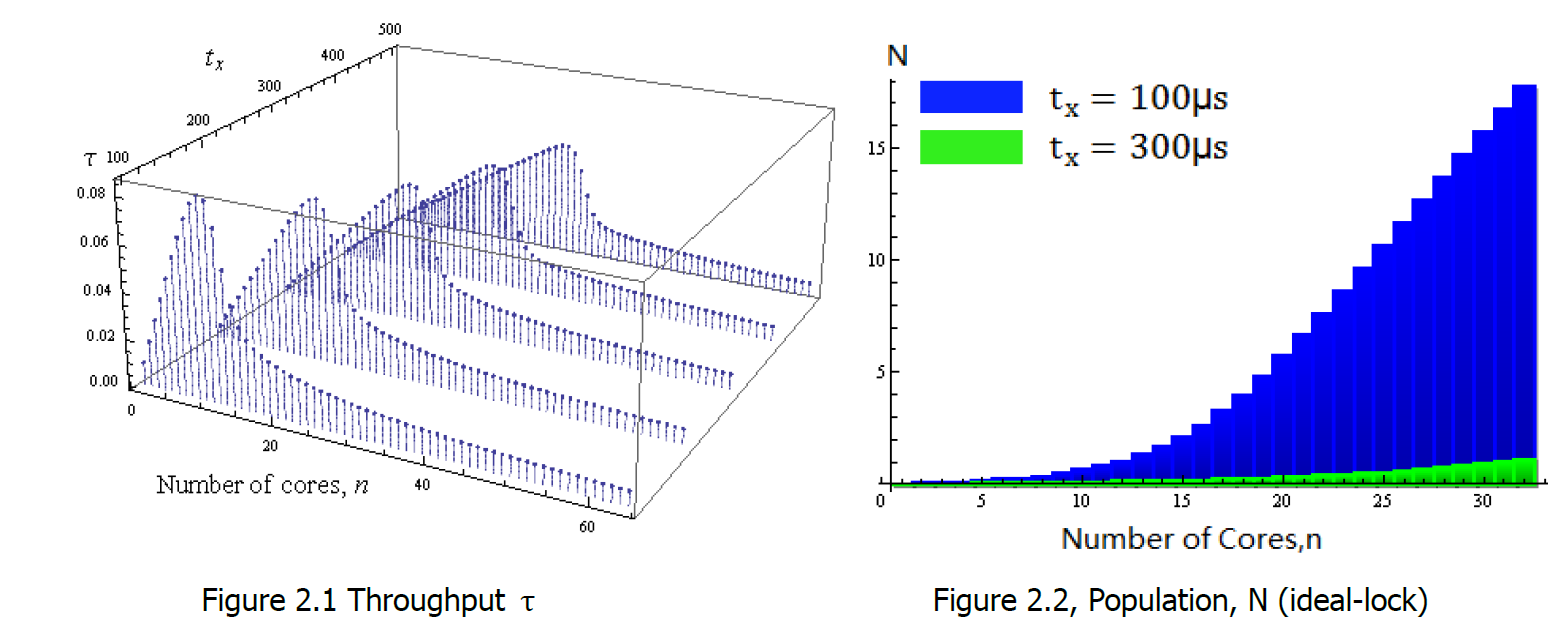
in average, hence it directly depends on number of cores executing or waiting at the moment. Thus, the more cores are waiting, the more time it takes to acquire the lock and vice versa (the more time it takes to acquire the lock the more cores will be waiting). The vicious cycle leads to the collapse in the speed-up. This means that adding additional cores to the process can result in steep decrease in performance instead of increasing it, as it seen in Figure 1.2.
In Figure 1.1, at t𝑥=300 μs, a small hump can be observed. This hump actually corresponds to the speed-up collapse. Figure 2.1 demonstrates five throughput plots according to t𝑥 values of 100, 200, 300, 400 and 500μs. It can be clearly seen that the exact number of cores corresponding to the following collapse becomes higher as t𝑥 increases.
As it can be seen in Figure 1.2 and Figure 1.3 whether ideal spinlock gives linear speed-up or not, clearly depends on the number of cores and parameters t𝑥, tc, tu. However, it is not a “perfectly” linear speed-up at any point. As it is demonstrated on the Figure 2.2, the population N is not constant, therefore the speed-up n-N apparently is not “perfectly” linear as n. Obviously, after certain point, increase in average number of cores either waiting or executing (N) becomes equal to increase in number of cores itself (n). At this point previously linear speed up hits the presumably never-ending plateau. According to approximation done as a part of this coursework the plateau occurs after number of cores reaches: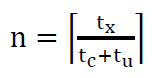 
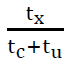
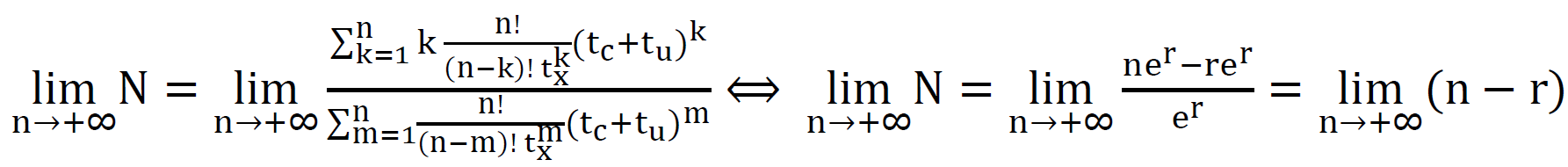
(accuracies are 90.13% and 91.41% for t𝑥=100 μs and t𝑥=300 μs respectively). Actually, the equation of “speed up” converges to the value of: 
This can be done by simplifying the population function which should be expressed in terms of tx, tc, and tu: 
where: 
In the model the tc – the average time spent in the critical section should depend on number of cores waiting for the lock. This due to the fact, that cores actually cache not only 2 bytes of the spinlock but the whole cache line which is 64 bytes for Intel Core i3-i7. The owner core needs an exclusive access to the cache line in order to write a value to the surrounding data. However, the other cores constantly acquiring a shared access to the spinlock cache line will prevent the owning core from acquiring abovementioned exclusive access. This will result in cache miss for every write operation performed by owning core to the spinlock cache line. The throughput can be reduced by a factor of two for k=1 and by a factor of 10 for k>1 (Corbet, J. 2013) [1].
Also, another model is that one core can be reserved as a dispatcher, passing inter-core messages and managing queues. However, the bigger gets number of managed critical sections the more complicated and “slow” gets the model due to the very limited cache size.
[1] Jonathan Corbet, (2013), “Improving ticket spinlocks”. Available at: http://lwn.net/Articles/531254/. Retrieved on 2013.10.29
